Once, I asked James Bond what was most important for a secret agent: shooting smartly or running quickly.

“None of them,” answered Bond. “The most important thing is to be invisible. You should not be noticed by anybody who is searching for you.”

“So, should you be dressed as a very average person?”

“Not exactly,” replied James. “Indeed, we considered what should be a kind of average clothing style, but we cannot outfit all agents in such a style. A long time ago, our hereditary princess suddenly disappeared during her visit to Rome. A hundred agents were simultaneously dispatched to Rome to find her.”

“I think I heard something about that…” I said.

Bond’s face suddenly hardened. “You could not have heard about that. It was top-secret.”

But then he softened a bit. “No matter, it’s an old story. So, we sent a hundred agents dressed as ‘average,’ but they all looked the same. When they disembarked from the plane, all the Italians greeted them with ‘buongiorno, signori agenti segreti !’ It was a complete fiasco. However, we learned from that case. You should not look ‘average’; you should deviate from the norm, but do it in a ‘usual’ way.”

“Some kind of random distribution?” I asked.

“Yes, but not just any random distribution,” Bond replied. “You should be distributed like a Gaussian curve around the average. That way, it’s difficult to catch you. Have you heard of Independent Component Analysis?”

“Is it about terrorists preparing explosions on Independence Day?” I guessed.

“Not exactly,” Bond smiled. “It’s a technique for identifying features distributed in an unusual way, such as anything that deviates from the Gaussian distribution, which is the most common in this world. Things that don’t follow a Gaussian pattern might be of interest to us. For example, detecting speech buried in a sea of noise. In fact, we rely on Independent Component Analysis more often than we do on our guns.”

Apply ICA to materials science

I was fascinated by what James Bond had said about Independent Component Analysis (ICA). I thought, maybe it could be applied to materials science, much like we had previously applied PCA. Perhaps ICA could even outperform PCA? I had come across an article claiming that ICA wasn’t very suitable for materials science, but honestly, its arguments didn’t convince me.

So, what is ICA? Like PCA, it involves rotations in a multidimensional factor space, but the way the basis is rotated differs. First and foremost, it’s essential to note that ICA always requires PCA as a preprocessing step. It begins by extracting the components with the highest variance, i.e., the principal components. However, it then does something unusual: it normalizes all components to have unity variance. The process called whitening equalizes the components, making it impossible to determine which ones are more principal and which are less. Subsequently, ICA once again rotates the basis, this time aiming to identify components with the highest non-Gaussianity. Mathematically, it can be demonstrated that such components are most likely independent of each other.

You might assume that ICA always produces independent components, while PCA does not. However, that’s not entirely accurate. In most cases, PCA components are also independent of each other, whereas ICA doesn’t always yield completely independent components. The difference lies more in the algorithms used for rotation within the factor space.

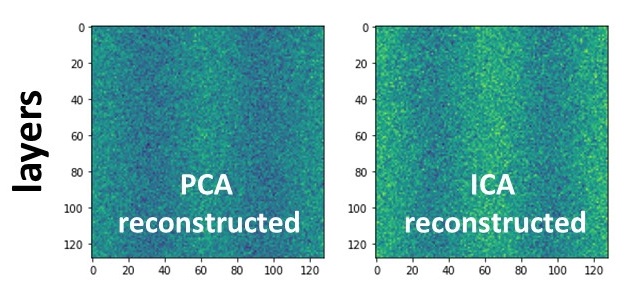
To highlight this difference, I generated two model datasets in which the composition smoothly transitions from phase A to phase B. In the first set, A and B represent layers, while in the second one, they appear as an atomic lattice. The crucial point is that the chemistry distribution from A to B is almost Gaussian for the lattice but strongly non-Gaussian for the layers.

For each pixel of the data, I generated a spectrum (consisting of 1000 channels) corresponding to its A/B fraction and added a significant amount of noise to obscure the original chemistry. When examining any energy slice of the generated spectrum-images, it becomes challenging to distinguish between A and B due to the noise. To make the maps visible, one must apply either PCA or ICA. Then, I made a remarkable observation: PCA and ICA perform equally well for the layers but not for the lattice. For the lattice, ICA fails entirely. This is because A and B are distributed as Gaussian in the lattice, and ICA cannot differentiate it from noise.

In conclusion, the success of ICA in materials science strongly depends on the inherent data distributions, which can vary widely in the field of materials science. In contrast, PCA does not concern itself with the distributions; it simply captures variations that exceed the noise level. Thus, the application of ICA in materials science is much more limited than, for instance, in speech recognition.

he Python codes can be found in the pdf version of this document: Full Text with Codes.