Once, I asked James Bond where his most difficult mission took place — was it in Turkey, Mexico, or Russia?
“In Great Britain, when I was promoted to the central analytical office of MI-6,” he answered.
“Were the headquarters suddenly attacked by an army of foreign spies?”
“I would have wished for that. Instead, I had to read endless reports from other secret agents abroad and try to understand what was going on.”
“Was that so difficult?”
“Mission impossible. Imagine this: some agent informs us that State X is planning to attack the UK on a certain date with all its ground, naval and air forces. Such an important message requires verification. Another agent confirms the dreadful plans of State X but claims they intend to attack State Y, not the UK. The third agent shares with us that State Y will indeed be soon invaded, but by State Z, not State X. What would you do when receiving hundreds of such messages?”
“I would kill myself. “

“I was on the verge of doing that. However, my older colleague advised me to relax, as he thought nobody was going to attack. We then developed a specific approach to understand the agents’ reports. You know, each agent is 100% confident in their information. However, this confidence is often subjective. We refer to this subjectivity as noise. Moreover, competing countries can intentionally fabricate and issue disinformation, which we call bias. All we need to do is collect a vast amount of data, calculate the noise (subjectivity) distribution, subtract the bias (disinformation), and extract the truth.”
“You’re suggesting that you calculate this using specific formulas? What might they look like?”
“No further comments. I can only provide you with one reference Secret Reference. If you read it carefully, you might gain an impression of how we handle big data.”
Evaluate accuracy of PCA
This conversation completely changed my understanding of how a secret service functions in reality. To delve deeper into the topic, I pursued Bond’s reference discovering an article by Noaz Nadler, a mathematician at the Weizmann Institute of Science. I thoroughly studied the article and attempted to verify its findings with some simulated spectrum-images.
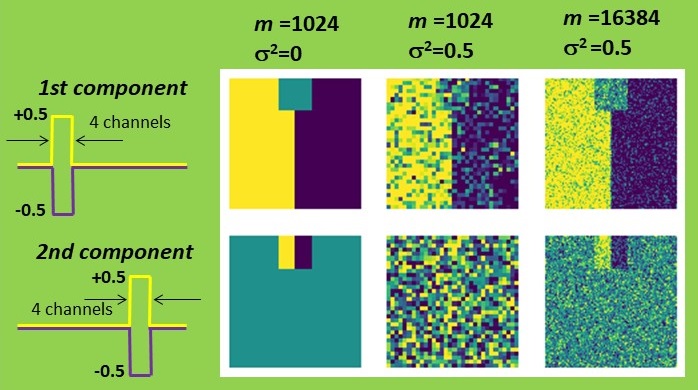
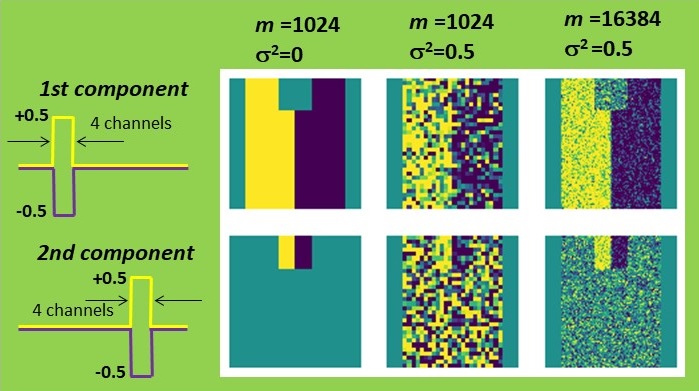
First, I constructed a simple dataset consisting of 32 by 32 pixels, each comprising 64 spectroscopic channels. The signal exhibited a rectangular shape and could be either positive or negative, resembling a characteristic line of a certain chemical element being emitted or absorbed. This signal variation is symmetric with a zero mean, simplifying the estimation process. The left half of the set was intended to represent the positive signal, while the right half represented the negative signal. One can map such a signal by summing all signal channels or by attempting to retrieve its distribution with PCA. Both methods yield identical results in the absence of noise. However, when Gaussian noise is introduced, PCA significantly outperforms simple summation. The result is still not perfect, but it appears quite reasonable.

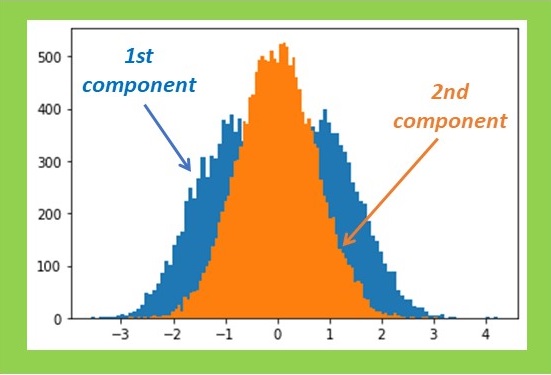
Now, a question arises: what is our criterion for estimating the accuracy of PCA? The simplest approach is to compare the shape of the PCA-recovered signal with the true one, which is precisely known in this case. Let’s sum the quadratic deviations over all channels and denote it as ∆2. Note that the appearance of the PCA-reconstructed maps correlates nicely with such a criterion: fewer deviations in the signal shape result in less noisy maps.

The cited paper suggests that PCA accuracy depends on the following parameters: the number of pixels m (32×32=1024 in our case), the number of channels n (64), the variance of noise σ2, and the variance of the true, noise-free signal α2. Calculating α2 might not be straightforward. I’ll just mention that it is exactly 1 in our case. Those interested in verifying this should refer to Exercise 1 in Full Text with Codes.
The paper then demonstrates that an error in PCA reconstruction is described very simply:


However, this simplicity holds true only for small σ2. The subsequent statement of the cited paper is even more instructive. When σ2 reaches a certain threshold, accuracy collapses to zero, ∆2 is undefined. There is no useful information in the dataset anymore; at least, nothing can be extracted by such a powerful method as PCA. This situation is reminiscent of James Bond’s troubles when too many contradictory reports actually provide no useful information.
The threshold for the loss of information is:

At this point, I apologize for inundating you with too many formulas. However, as you see in the modern world, even secret agents are increasingly relying on formulas rather than old-fashioned master keys in their work.
Now, back to our business! I validated the theory by altering the number of pixels m and the noise level σ2 in my dataset. In all cases, PCA accuracy improved as m increased or σ2 decreased, precisely as predicted. Moreover, when the combination of parameters reached the magic Nadler ratio (2), the maps became irretrievable.

For those interested in further testing the Nadler model, I have prepared Exercises 2 and Exercise 3 in Full Text with Codes. The Python codes are attached. Have fun!
Leave a Reply